2020-06-10

Interactive Sorting (Language Test 202001 L)

問題

L - Interactive Sorting

解法

$N = 26$ のケースではマージソートを行なえばいいです．以下では $N = 5, Q = 7$ のケースを扱います．

前提知識

ソートアルゴリズムは木で表現できます．例えば，相異なる3つの要素に対するマージソート *1は次のように表せます．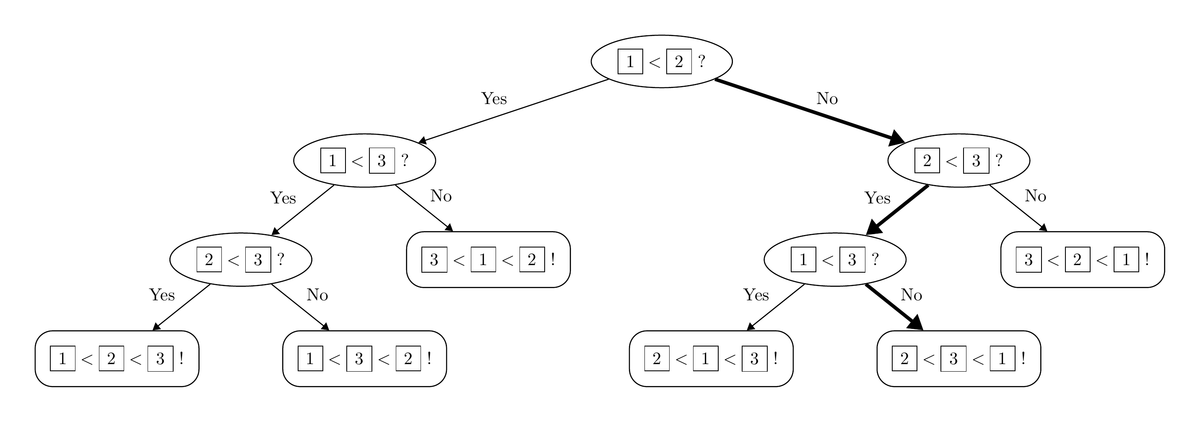

葉以外の頂点（丸い頂点）は要素の比較を表し，葉（四角い頂点）は求めた大小関係の出力を表しています．また，四角で囲われた番号は元の配列における要素の番号です．要素を交換した後の番号ではないことに注意してください．

例えば，太線で示したパスを追うと，

1番目の要素と2番目の要素を比較する．2番目の要素の方が小さいことが分かる
（元の配列における）2番目の要素と3番目の要素を比較する．2番目の要素の方が小さいことが分かる．結果として2番目の要素が最小であることが分かる
1番目の要素と3番目の要素を比較する．3番目の要素の方が小さいことが分かる
求めた大小関係として「2番目の要素，3番目の要素，1番目の要素」を出力する

各頂点に対して，それに至る要素の大小関係を書くと次のようになります．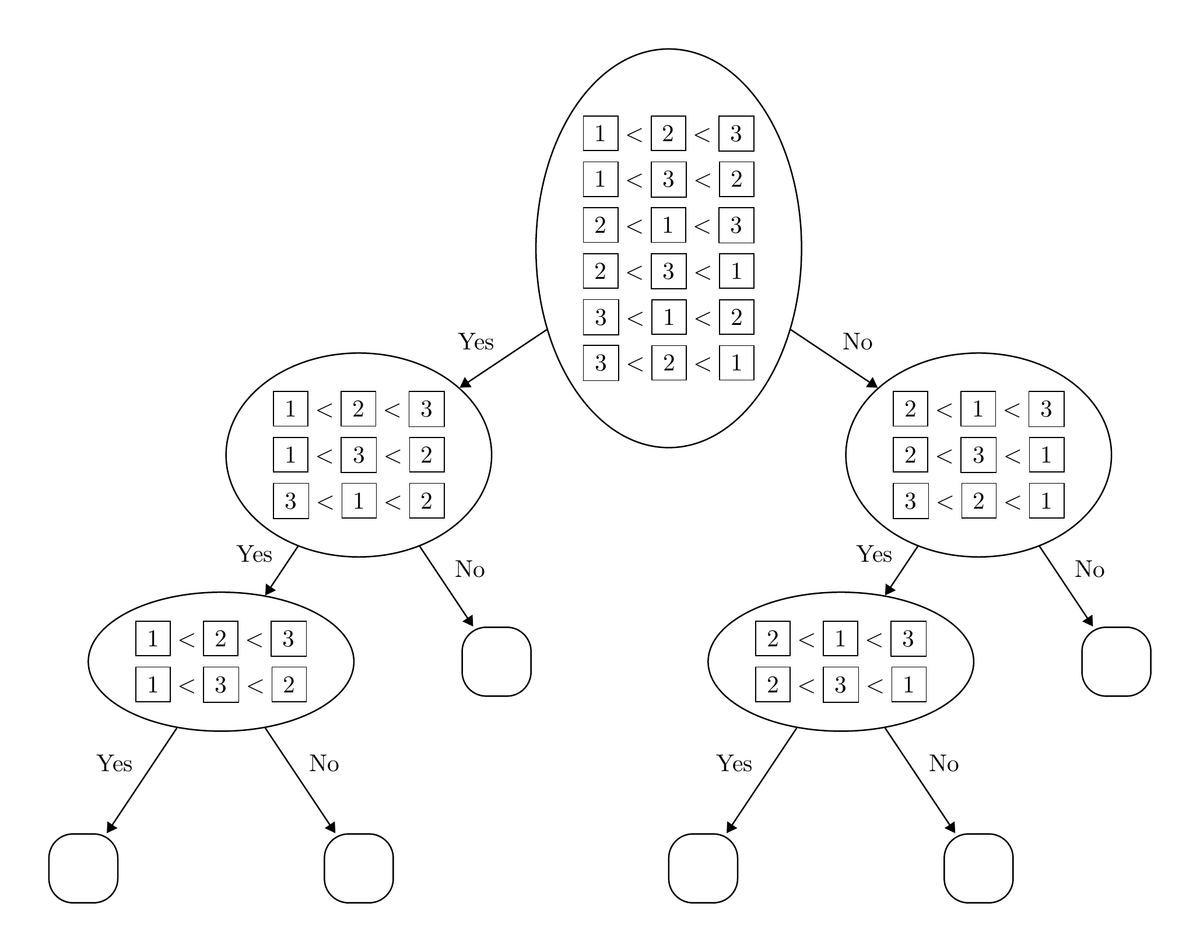

考察に使うソートアルゴリズムの木の性質は次の2つです：

木の高さはソートに必要な（最大の）比較回数に等しい
木の高さを $h$ とすると，出力される大小関係は最大でも $2^h$ 個しかない

考察

ソートアルゴリズムが制約を満たすための必要条件として次の2つが得られます：

比較は最大で 7 回しかできないので，木の高さは 7 以下でなければならない
各頂点について，それに至る要素の大小関係はすべてその頂点を根とする部分木の葉で出力されなければならない．そのため，大小関係の個数が部分木の葉の個数以下でなければならない．特に注目している頂点の深さを $d$ とすると，大小関係の個数は $2^{7-d}$ 以下でなければならない

この必要条件を元に制約を満たすソートアルゴリズム（の木）を見つけることを考えます．

5要素の大小関係は $5! = 120$ 通りあります．一方で，高さ 7 の木の葉の個数は $2^7 = 128$ 以下です．これら2つの数が近いことから，規定回数以内にソートするのは難しいと予想できます．逆に言えば，条件が厳しいので，探索空間が小さいことが期待できます．この段階で探索を書き始めてもいいのですが，より確信を得るために考察を進めます．

1回目の比較

（どの要素も対等なので）1番目の要素と2番目の要素を比較することにします
1番目の要素の方が小さい場合を考えます（2番目の要素の方が小さい場合も同様の考察ができます）
120 個の大小関係のうち，そのようなものは 60 個あります
高さ 6 の木の葉は最大で $2^6 = 64$ 個しかないので，依然としてギリギリです

2回目の比較

1番目の要素，2番目の要素のいずれかとそれ以外の要素を比較するとうまく行きません
- 例えば，1番目の要素と3番目の要素を比較したとします
- 60 個の大小関係のうち，1番目の要素の方が小さいものは 40 個，そうでないものは 20 個あります（前者は3番目までの要素の大小関係が2通りあるのに対して，後者は1通りしかない）
- 高さ 5 の木の葉は最大で $2^5 = 32$ 個しかなく， $32 < 40$ なので，正しくソートされないケースが出てきてしまいます
- その他の場合も同様の理由でうまく行きません
もちろん再び1番目の要素，2番目の要素を比較するのはうまく行きません．
結局，3番目以降の要素を比較するしかないことが分かります．（それらの要素は対等なので）3番目の要素と4番目の要素を比較することにします
3番目の要素の方が小さい場合を考えます
60 個の大小関係のうち，そのようなものは 30 個あります

3回目の比較

5番目の要素と他の要素を比較するとうまく行かないことが2回目の考察と同様にして分かります
1番目の要素と4番目の要素の比較（，2番目の要素と3番目の要素の比較）もうまく行かないことが分かります
- 30 個の大小関係のうち，1番目の要素の方が小さいものは 25 個，そうでないものは 5 個あります
- 高さ 4 の木の葉は最大で $2^4 = 16$ 個しかなく， $16 < 25$ なので，正しくソートされないケースが出てきてしまいます
したがって，1番目の要素と3番目の要素，あるいは，2番目の要素と4番目の要素を比較するしかないことが分かります．そこで前者を比較することにします
1番目の要素の方が小さい場合を考えます
30 個の大小関係のうち，そのようなものは 15 個あります
15 と 16 の間には差が 1 しかなく，今までの考察を踏まえると条件を満たすのは極めて難しそうです
結論として，探索空間が小さいことが期待でき，条件を満たす木を1つだけ見つけるのは高速にできそうです

実装

考察を元に実装したソースコードを下に示します．木を扱いやすいこと，1つだけ取り出す操作が書きやすいことから Haskell で書いています．

trees関数：条件を満たす木を列挙する
- min (length ys) (length zs) == length xs `div` 2は大小関係の個数と葉の個数に関する条件です（上述の必要条件より強い）
tree：trees関数が見つけた最初の木
- （デフォルトの）Haskell は遅延評価を行なうので，すぐに計算できます*2
special関数：treeに従ってソートを行なう

余談

$N$ 要素の大小関係は $N!$ 通りあるので，すべての大小関係に対して正しくソートするためには少なくとも $\lceil \log_{2}(N!) \rceil$ 回の比較が必要です．では，その回数以内の比較で必ずソートできるのでしょうか？OEIS に $N$ 要素をソートするために必要な最小の比較回数が載っていた（A036604 - OEIS）ので，その回数と $\lceil \log_{2}(N!) \rceil$ を比べてみると次のようになります．

$N$	1	2	3	4	5	6	7	8	9	10	11	12
最小の比較回数	0	1	3	5	7	10	13	16	19	22	26	30
$\lceil \log_{2}(N!) \rceil$	0	1	3	5	7	10	13	16	19	22	26	29

$N = 12$ が反例になるので，必ずしも可能でないことが分かります．

*1: (1) 3つの要素を2つと1つに分ける，(2) 2要素のグループをソートする（＝比較して，必要ならば，交換する），(3) 2つのグループの先頭から小さい要素を取り出すことを繰り返す

*2:Haskell に詳しくないので正しい説明になっているか自信がないです

2019-05-04

Card Game II (AOJ 0504)

もう3月も前のことですが，AOJのVol. 5を埋め終わりました．この問題の解説はあまり見ないので，その記念に書こうと思います．競プロを始めた頃はややこしい数学ゲーという印象がありましたが，意外とすっと解けます．

問題

カードゲーム | Aizu Online Judge

解法

ゲームで引く順番にカードを並べると数列が1つ得られます．ちょうど $m$ 回の再開で成功したとき，この数列がどうなっているかを考えます．

$m = 0$ のとき

最初に山 $1$ のカードを引いた後，山 $i$ からカードを引くためには数 $i$ が書かれたカードを引く必要があります．そのため，山 $1$ のカードをすべて引くにはそれより1枚少ない枚数の $1$ の書かれたカードを引く必要があり，山 $i \ (i \ge 2)$ のカードをすべて引くにはそれと同じ枚数の $i$ の書かれたカードを引く必要があります．その後，その山でゲームを終了するには同じカードをさらに1枚引く必要があります．ゲーム開始時，数 $i$ が書かれたカードは山 $i$ のカードと同じ枚数しかなかったので，2番目以降の山でゲームを終了するにはカードが足りません．したがって，最後に引いたカードには $1$ が書かれています．

$m = 1$ のとき

同様の考察から失敗する直前に引いたカードには $1$ が書かれていることが分かります．これは山 $1$ からカードを引こうとして失敗したことを意味するので，山 $1$ のカードと $1$ の書かれたカードは失敗するまでにすべて引かれています．山 $i \ (i \ge 2)$ のカードと数 $i$ が書かれたカードについては引いた枚数が同じなので，残る枚数も同じです．特に再開後最初にカードを引いた山の番号を $b \ (b \ge 2)$ とすると，山 $i \ (2 \le i < b)$ のカードはすべて引かれているので， $i$ の書かれたカードもすべて引かれています．ゲーム再開時の山 $i$ のカードと数 $i$ が書かれたカードの残り枚数は同じなので，最初と同じ考察ができて，ゲームの最後に引いたカードには $b$ が書かれていることが分かります．

以上により，ゲームで得られる数列は

$m = 0$ のとき：最後は $1$ で終わる（条件1）
$m = 1$ のとき： $2$ 以上 $n$ 以下の整数 $b$ が存在し， $b$ 未満の数の中で最も後ろにあるのは $1$ で，最後は $b$ で終わる（条件2）

を満たすことが分かりました．

逆にこれらの条件を満たす数列からその数列が得られるちょうど $m$ 回の再開で成功する配置を作ることができます．例えば，条件1を満たす数列が与えられたとき，1番目の数が書かれたカードを山 $1$ に置き，2番目以降の数が書かれたカードをその直前の数の山に置くことで，再開なしで成功する配置が得られます．この対応は1対1対応なので，条件1，2を満たす数列を数えればよくなります．

条件1を満たす数列の個数 $C$ は

$\begin{align*}C = \frac{(nk-1)!}{(k-1)!(k!)^{n-1}}\end{align*}$

です．

各 $b = 2, 3, \dots, n$ に対して，条件2を満たす数列の個数 $C_{b}$ は

$\begin{align*}C_{b} = \frac{(nk-1)!}{((b-1)k)!(k-1)!(k!)^{n-b}} \cdot \frac{((b-1)k-1)!}{(k-1)!(k!)^{b-2}} = \frac{(nk-1)!}{(b-1)(k-1)!(k!)^{n-1}} = \frac{C}{b-1}\end{align*} \$

です．これは $b$ 未満の数をまとめて扱い，その後で分けて扱うことで得られます．

可能な配置は $(nk)! / (k!)^{n} = nC$ 個あります．

最後に簡単な計算をすることで，求める確率が

$m = 0$ のとき： $1 / n$
$m = 1$ のとき： $1 / n + \sum_{b=2}^{n} 1 / ((b-1)n)$

であることが分かります．

#include <bits/stdc++.h>

#define fst(t) std::get<0>(t)
#define snd(t) std::get<1>(t)
#define thd(t) std::get<2>(t)
#define unless(p) if(!(p))
#define until(p) while(!(p))

using ll = std::int64_t;
using P = std::tuple<int,int>;

template <int r>
struct Decimal{
    std::vector<int> digits;
    
    Decimal(int n) : digits(r + 1, 0) { // 1/n
        int rem = 1;
        for(int i=1;i<=r;++i){
            rem *= 10;
            digits[i] = rem / n;
            rem %= n;
        }
    }

    Decimal<r>& operator+=(Decimal<r> &rhs){
        for(int i=r;i>0;--i){
            digits[i] += rhs.digits[i];
            if(digits[i] >= 10){
                digits[i] -= 10;
                digits[i - 1] += 1;
            }
        }

        return *this;
    }
};

constexpr int r = 10100;

int main(){
    std::cin.tie(nullptr);
    std::ios::sync_with_stdio(false);

    while(true){
        int N, K, M, R;
        std::cin >> N >> K >> M >> R;

        if(N == 0){
            break;
        }

        Decimal<r> p(N);

        if(M == 1){
            for(int k=1;k<=N-1;++k){
                Decimal<r> d(k * N);
                p += d;
            }
        }

        std::cout << p.digits[0] << ".";
        for(int i=1;i<=R;++i){
            std::cout << p.digits[i];
        }
        std::cout << std::endl;
    }
}

2018-12-01

Educational Codeforces Round #55 F - Speed Dial

問題文: https://codeforces.com/contest/1082/problem/F

s[i] をソートして，Trieの代わりにしようとすると，（うまくやらない限り）

で落ちるかもしれません（自分は落ちました）．両端のために01，真ん中2つのために012のボタンを用意すると，2回でできるんですね．

ケースを書くだけで，雑ですが，書いておきます．

2015-04-01

虚空と光明のディスクール(HARD MODE) - jin_matakich 強化コンテスト(extended) F

かしこいかわいいBIT．

解法

X方向の加算，Y方向の加算に分ける．
それぞれについて，左(上)との差を考えると，区間への加算，区間和を求めることができればいいと分かる．
これはBITやSegment Treeでできる．imos法+累積和でもできるらしい．

コード

ライブラリ部分は省略しています．

// Wrongri-La Shower

#include <cstdio>
#include <array>

typedef long long ll;

template <typename T, int n>
class BIT{};

template <typename T, int n>
class CuteCleverBIT{};

int W, H, N, Q;
// bits: X, bits2: Y
CuteCleverBIT<ll,3000> bits[3001], bits2[3001];
ll map[3001][3001];

int main(){
    scanf("%d %d %d %d", &W, &H, &N, &Q);

    for(int i=0;i<N;i++){
        int x, y, a;
        scanf("%d %d %d", &x, &y, &a);

        int l = std::max(x-a+1, 1), r = std::min(x+a-1, W),
            t = std::max(y-a+1, 1), b = std::min(y+a-1, H);

        bits[y].add(l, l+1, a-(x-l));
        bits[y].add(l+1, x+1, 1);
        bits[y].add(x+1, r+2, -1);

        bits2[x].add(t, t+1, a-(y-t));
        bits2[x].add(t+1, y, 1);
        bits2[x].add(y, y+1, -(a-1));
        bits2[x].add(y+1, y+2, a-1);
        bits2[x].add(y+2, b+2, -1);
    }

    for(int i=1;i<=H;i++){
        for(int j=1;j<=W;j++){
            map[i][j] = bits[i].sum(j+1);
        }
    }

    for(int i=1;i<=W;i++){
        for(int j=1;j<=H;j++){
            map[j][i] += bits2[i].sum(j+1);
        }
    }

    for(int i=0;i<Q;i++){
        int x, y;
        scanf("%d %d", &x, &y);

        printf("%lld\n", map[y][x]);
    }
}

2015-03-28

YukiCoder No.162 - 8020運動

想定誤解法らしい．(システムテストに目をつけられたら落ちそう．)

解法

上下の歯は独立しているので，上の歯14本だけを考える．
あらかじめ，歯の状態間の遷移確率を計算しておく．
配るdp[年齢][歯の状態(bit表現)]をする．20・2^14・2^14(≒5.3x10^9)でΩ\・8・)ﾁｭｰﾝだが，実はΩ\・8・)ﾁｭｰﾝでもない．
1歳老いるときの配る回数を考える．ある歯の状態からの遷移先は2^(生存している歯の本数)個ある．
(生存しているそれぞれの歯に対して，生存させるか，させないかの2通りがあるから．)
なので，配る回数は
$\displaystyle \sum_{k=0}^{14}({}_{14}C_{k} \, 2^{k})$
と表せる．
括弧内を落ち着いて見ると，「14個からk個選んで，それらに0，1のいずれかを入れる方法の総数」と解釈できる．
全体をゆったり眺めると，「14個のマスに0，1，つかわないのいずれかを割り当てる方法の総数」と解釈できる．これは14桁の3進数の個数，すなわち，3^14に等しい．
ゆえに配る回数の総数は20・3^14(≒9.5x10^7)となるので(前処理が重いので1[s]は超えるが)間に合う．

[追記(15/03/28 22:33)]
落ち着いて見なくても，ゆったり眺めなくても，2項定理から
$\displaystyle \sum_{k=0}^{14}({}_{14}C_{k} \, 2^{k}) = \sum_{k=0}^{14}({}_{14}C_{k} \, 2^{k} \, 1^{14-k}) = (1+2)^{14} = 3^{14}$
と求められます．くろとんさんに教えていただきました．ありがとうございました．
[追記おわり]

コード

// Wrongri-La Shower

#include <cstdio>
#include <vector>

typedef std::pair<int,double> Pair;

double P[3]; // 虫歯に「なる」確率
std::vector<Pair> ns[1<<14];
double dp[21][1<<14];

double probability(int prev, int next){
    double res = 1.0;
    for(int i=0;i<14;i++){
        if(!(prev >> i & 1)){continue;}
        
        double p;
        if(i == 0){
            p = P[prev >> 1 & 1];
        }else if(i == 13){
            p = P[prev >> 12 & 1];
        }else{
            p = P[(prev >> i-1 & 1) + (prev >> i+1 & 1)];
        }

        res *= next >> i & 1 ? 1.0-p : p;
    }

    return res;
}

int main(){
    int N;
    scanf("%d", &N);
    N = 80-N;

    scanf("%lf %lf %lf", P, P+1, P+2);
    for(int i=0;i<3;i++){P[i] /= 100;}

    
    for(int i=0;i<1<<14;i++){
        for(int j=0;j<1<<14;j++){
            if((i & j) != j){continue;}

            ns[i].push_back(std::make_pair(j, probability(i, j)));
        }
    }

    dp[0][(1<<14)-1] = 1.0;
    for(int i=0;i<N;i++){
        for(int j=0;j<1<<14;j++){
            for(const auto& p : ns[j]){
                dp[i+1][p.first] += dp[i][j] * p.second;
            }
        }
    }

    double res = 0.0;
    for(int i=0;i<1<<14;i++){
        res += dp[N][i] * __builtin_popcount(i);
    }

    printf("%.12f\n", res * 2);
}

2015-03-26

YukiCoder No.54 - Happy Hallowe'en

何か解けちゃった．

解法

最大値を伝搬させていく．mx[n] := お菓子n個から最大何個とれるかとする．
最初はmx[n] = nとする．各iに対して，
mx[j] = max(mx[j], mx[j+V[i]]) (jはj < T[i]を満たすすべての非負整数)
と更新する．
iの選ぶ順序を工夫しなければならないが，T[i]+V[i]の大きい順にやればいい．
これは大きい値をもってくるものを先にやるとよさそうだということから予想できる．(適当に不等式をこねると証明できるらしい．)
計算量はO(N log N + N T_max)．N<=10^4，T_max<=10^4だが，YukiCoderは偉大なので十分に間に合う．

コード

// Wrongri-La Shower

#include <cstdio>
#include <algorithm>
#include <utility>

typedef std::pair<int,int> P;
typedef std::pair<int,P> Q;

int N;
int V[10000], T[10000];

int solve(){
    Q ps[10000];

    for(int i=0;i<N;i++){
        ps[i] = std::make_pair(T[i]+V[i], std::make_pair(T[i], V[i]));
    }
    std::sort(ps, ps+N);
    std::reverse(ps, ps+N);
    
    int mx[20001];
    for(int i=0;i<=20000;i++){
        mx[i] = i;
    }

    for(int i=0;i<N;i++){
        const P& p = ps[i].second;
        for(int j=0;j<p.first;j++){
            if(j+p.second > 20000){continue;}
            mx[j] = std::max(mx[j], mx[j+p.second]);
        }
    }
    
    return mx[0];
}

int main(){
    scanf("%d", &N);

    for(int i=0;i<N;i++){
        scanf("%d %d", V+i, T+i);
    }

    printf("%d\n", solve());
}

2015-03-21

AOJ 0091 - Blur

3^n系だ．いい問題だと思います．

解法

全探索．
左上から右下に走査し，染められている場所を探す．
その場所を(x, y)とすると，そこを染めるには
(x, y+1)から「小」を垂らす
(x+1, y+1)から「中」を垂らす
(x, y+2)から「大」を垂らす
の3通りがある．これらをすべて試すのを繰り返す．
3つともダメだったらできない．

場所探しはO(WH)，毎回3通りの染め方を試すので，計算量はO(3^N W H)(だと思います．間違ってたらご指摘ください．)

コード

塗ったり，塗れるかを試すときはマンハッタン距離をつかうといいかも．

#include <cstdio>
#include <algorithm>
#include <string>

const int dx[3] = {0, 1, 0}, dy[3] = {1, 1, 2};
int N;
int cloth[10][10];
int x[12], y[12], type[12];

bool canFill(int cx, int cy, int t){
    int mx;
    
    if(t == 0){
        mx = 1;
    }else if(t == 1){
        mx = 2;
    }else if(t == 2){
        mx = 2;
    }

    for(int i=-mx;i<=mx;i++){
        for(int j=-mx;j<=mx;j++){
            if(std::abs(i) + std::abs(j) > mx){continue;}
            if(t == 1 && (i == 0 && std::abs(j) == 2 || std::abs(i) == 2 && j == 0)){continue;}
            int x = j + cx, y = i + cy;
            if(x < 0 || x >= 10 || y < 0 || y >= 10){return false;}
            if(!cloth[y][x]){return false;}
        }
    }

    return true;
}

void spuit(int cx, int cy, int t, int v){
    int mx;
    
    if(t == 0){
        mx = 1;
    }else if(t == 1){
        mx = 2;
    }else if(t == 2){
        mx = 2;
    }

    for(int i=-mx;i<=mx;i++){
        for(int j=-mx;j<=mx;j++){
            if(std::abs(i) + std::abs(j) > mx){continue;}
            if(t == 1 && (i == 0 && std::abs(j) == 2 || std::abs(i) == 2 && j == 0)){continue;}
            int x = j + cx, y = i + cy;
            if(x < 0 || x >= 10 || y < 0 || y >= 10){continue;}
            cloth[y][x] -= v;
        }
    }
}

bool dfs(int n){
    if(n == N){
        for(int i=0;i<10;i++){
            for(int j=0;j<10;j++){
                if(cloth[i][j]){return false;}
            }
        }
        
        for(int i=0;i<N;i++){
            printf("%d %d %d\n", x[i], y[i], type[i]);
        }
        return true;
    }

    for(int i=0;i<10;i++){
        for(int j=0;j<10;j++){
            if(!cloth[i][j]){continue;}
            for(int k=0;k<3;k++){
                int cx = j + dx[k], cy = i + dy[k];
                if(!canFill(cx, cy, k)){continue;} 
                spuit(cx, cy, k, 1);
                
                x[n] = cx; y[n] = cy; type[n] = k + 1;
                if(dfs(n+1)){return true;}
                spuit(cx, cy, k, -1);       
            }
            return false;
        }
    }

    return false;
}

int main(){
    scanf("%d", &N);

    for(int i=0;i<10;i++){
        for(int j=0;j<10;j++){
            scanf("%d", &cloth[i][j]);
        }
    }
    
    dfs(0);
}