Interactive Sorting (Language Test 202001 L)

問題

L - Interactive Sorting

解法

$N = 26$ のケースではマージソートを行なえばいいです．以下では $N = 5, Q = 7$ のケースを扱います．

前提知識

ソートアルゴリズムは木で表現できます．例えば，相異なる3つの要素に対するマージソート *1は次のように表せます．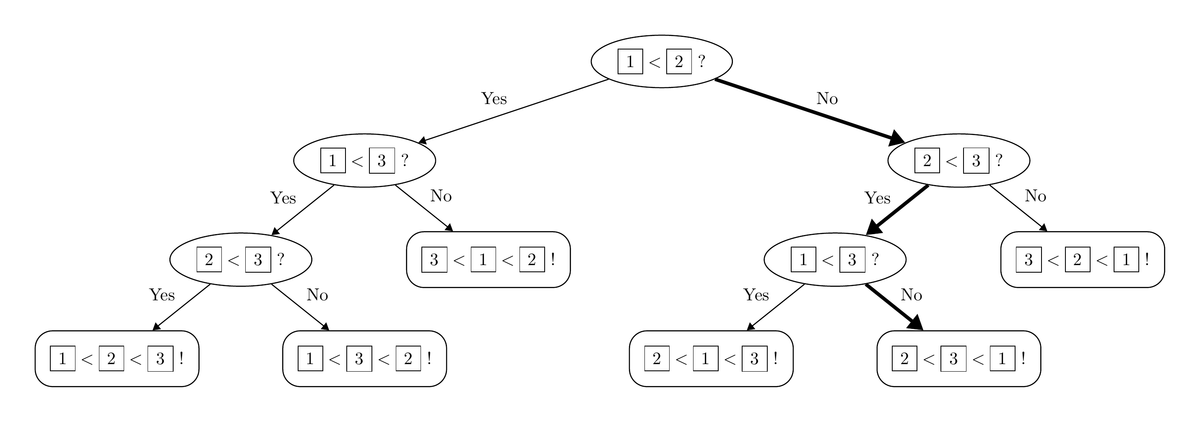

葉以外の頂点（丸い頂点）は要素の比較を表し，葉（四角い頂点）は求めた大小関係の出力を表しています．また，四角で囲われた番号は元の配列における要素の番号です．要素を交換した後の番号ではないことに注意してください．

例えば，太線で示したパスを追うと，

1番目の要素と2番目の要素を比較する．2番目の要素の方が小さいことが分かる
（元の配列における）2番目の要素と3番目の要素を比較する．2番目の要素の方が小さいことが分かる．結果として2番目の要素が最小であることが分かる
1番目の要素と3番目の要素を比較する．3番目の要素の方が小さいことが分かる
求めた大小関係として「2番目の要素，3番目の要素，1番目の要素」を出力する

各頂点に対して，それに至る要素の大小関係を書くと次のようになります．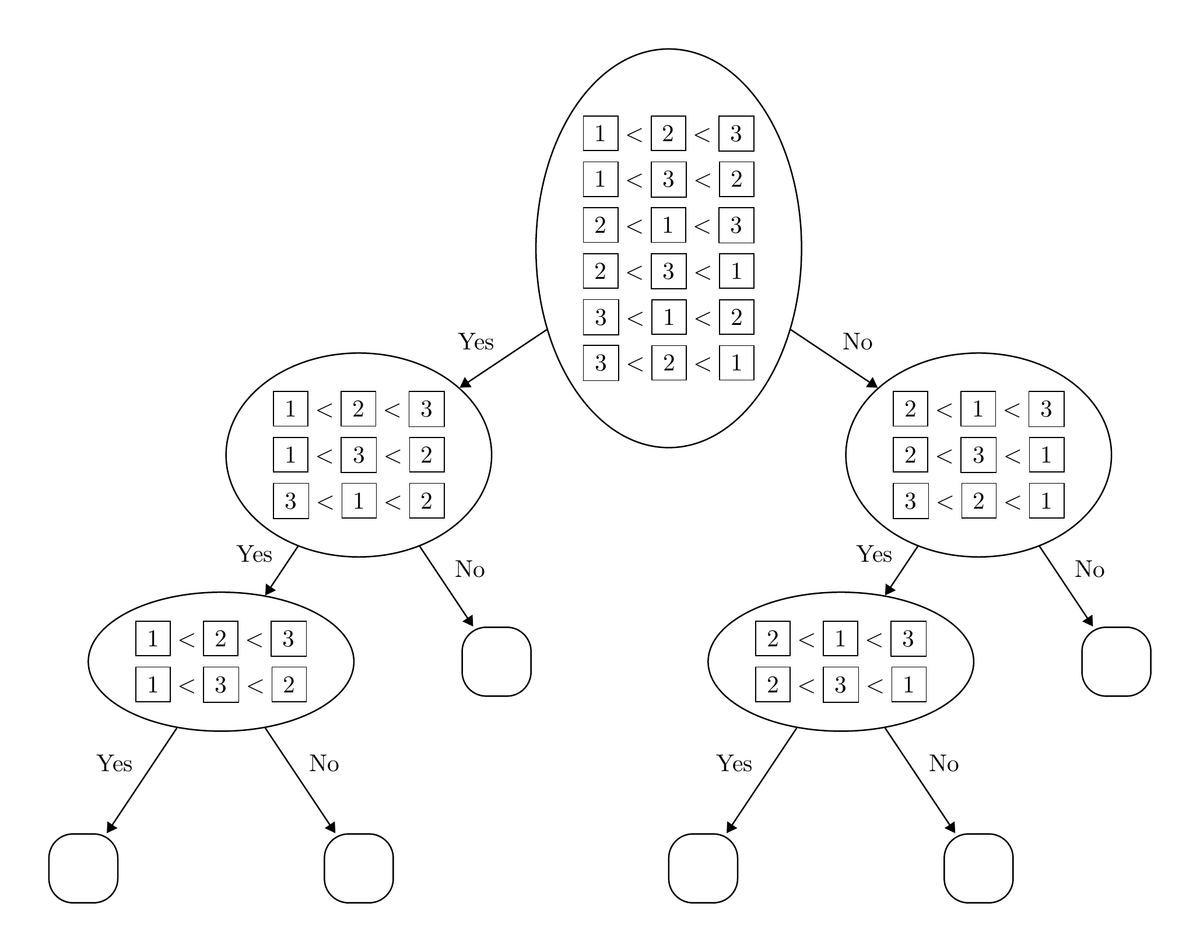

考察に使うソートアルゴリズムの木の性質は次の2つです：

木の高さはソートに必要な（最大の）比較回数に等しい
木の高さを $h$ とすると，出力される大小関係は最大でも $2^h$ 個しかない

考察

ソートアルゴリズムが制約を満たすための必要条件として次の2つが得られます：

比較は最大で 7 回しかできないので，木の高さは 7 以下でなければならない
各頂点について，それに至る要素の大小関係はすべてその頂点を根とする部分木の葉で出力されなければならない．そのため，大小関係の個数が部分木の葉の個数以下でなければならない．特に注目している頂点の深さを $d$ とすると，大小関係の個数は $2^{7-d}$ 以下でなければならない

この必要条件を元に制約を満たすソートアルゴリズム（の木）を見つけることを考えます．

5要素の大小関係は $5! = 120$ 通りあります．一方で，高さ 7 の木の葉の個数は $2^7 = 128$ 以下です．これら2つの数が近いことから，規定回数以内にソートするのは難しいと予想できます．逆に言えば，条件が厳しいので，探索空間が小さいことが期待できます．この段階で探索を書き始めてもいいのですが，より確信を得るために考察を進めます．

1回目の比較

（どの要素も対等なので）1番目の要素と2番目の要素を比較することにします
1番目の要素の方が小さい場合を考えます（2番目の要素の方が小さい場合も同様の考察ができます）
120 個の大小関係のうち，そのようなものは 60 個あります
高さ 6 の木の葉は最大で $2^6 = 64$ 個しかないので，依然としてギリギリです

2回目の比較

1番目の要素，2番目の要素のいずれかとそれ以外の要素を比較するとうまく行きません
- 例えば，1番目の要素と3番目の要素を比較したとします
- 60 個の大小関係のうち，1番目の要素の方が小さいものは 40 個，そうでないものは 20 個あります（前者は3番目までの要素の大小関係が2通りあるのに対して，後者は1通りしかない）
- 高さ 5 の木の葉は最大で $2^5 = 32$ 個しかなく， $32 < 40$ なので，正しくソートされないケースが出てきてしまいます
- その他の場合も同様の理由でうまく行きません
もちろん再び1番目の要素，2番目の要素を比較するのはうまく行きません．
結局，3番目以降の要素を比較するしかないことが分かります．（それらの要素は対等なので）3番目の要素と4番目の要素を比較することにします
3番目の要素の方が小さい場合を考えます
60 個の大小関係のうち，そのようなものは 30 個あります

3回目の比較

5番目の要素と他の要素を比較するとうまく行かないことが2回目の考察と同様にして分かります
1番目の要素と4番目の要素の比較（，2番目の要素と3番目の要素の比較）もうまく行かないことが分かります
- 30 個の大小関係のうち，1番目の要素の方が小さいものは 25 個，そうでないものは 5 個あります
- 高さ 4 の木の葉は最大で $2^4 = 16$ 個しかなく， $16 < 25$ なので，正しくソートされないケースが出てきてしまいます
したがって，1番目の要素と3番目の要素，あるいは，2番目の要素と4番目の要素を比較するしかないことが分かります．そこで前者を比較することにします
1番目の要素の方が小さい場合を考えます
30 個の大小関係のうち，そのようなものは 15 個あります
15 と 16 の間には差が 1 しかなく，今までの考察を踏まえると条件を満たすのは極めて難しそうです
結論として，探索空間が小さいことが期待でき，条件を満たす木を1つだけ見つけるのは高速にできそうです

実装

考察を元に実装したソースコードを下に示します．木を扱いやすいこと，1つだけ取り出す操作が書きやすいことから Haskell で書いています．

trees関数：条件を満たす木を列挙する
- min (length ys) (length zs) == length xs `div` 2は大小関係の個数と葉の個数に関する条件です（上述の必要条件より強い）
tree：trees関数が見つけた最初の木
- （デフォルトの）Haskell は遅延評価を行なうので，すぐに計算できます*2
special関数：treeに従ってソートを行なう

余談

$N$ 要素の大小関係は $N!$ 通りあるので，すべての大小関係に対して正しくソートするためには少なくとも $\lceil \log_{2}(N!) \rceil$ 回の比較が必要です．では，その回数以内の比較で必ずソートできるのでしょうか？OEIS に $N$ 要素をソートするために必要な最小の比較回数が載っていた（A036604 - OEIS）ので，その回数と $\lceil \log_{2}(N!) \rceil$ を比べてみると次のようになります．

$N$	1	2	3	4	5	6	7	8	9	10	11	12
最小の比較回数	0	1	3	5	7	10	13	16	19	22	26	30
$\lceil \log_{2}(N!) \rceil$	0	1	3	5	7	10	13	16	19	22	26	29

$N = 12$ が反例になるので，必ずしも可能でないことが分かります．

*1: (1) 3つの要素を2つと1つに分ける，(2) 2要素のグループをソートする（＝比較して，必要ならば，交換する），(3) 2つのグループの先頭から小さい要素を取り出すことを繰り返す

*2:Haskell に詳しくないので正しい説明になっているか自信がないです